We are interested in problems where an accurate description of electronic correlations is important. The main theoretical/computational tool we employ is the quantum Monte Carlo method.
A great advantage of quantum Monte Carlo methods is that one has considerable freedom in the choice of the trial wave function. So, any intuition one has for the many-body wave function can be tested out. In order to best exploit its potential advantages, we have invested considerable time in improving various aspects of quantum Monte Carlo methodology. These include
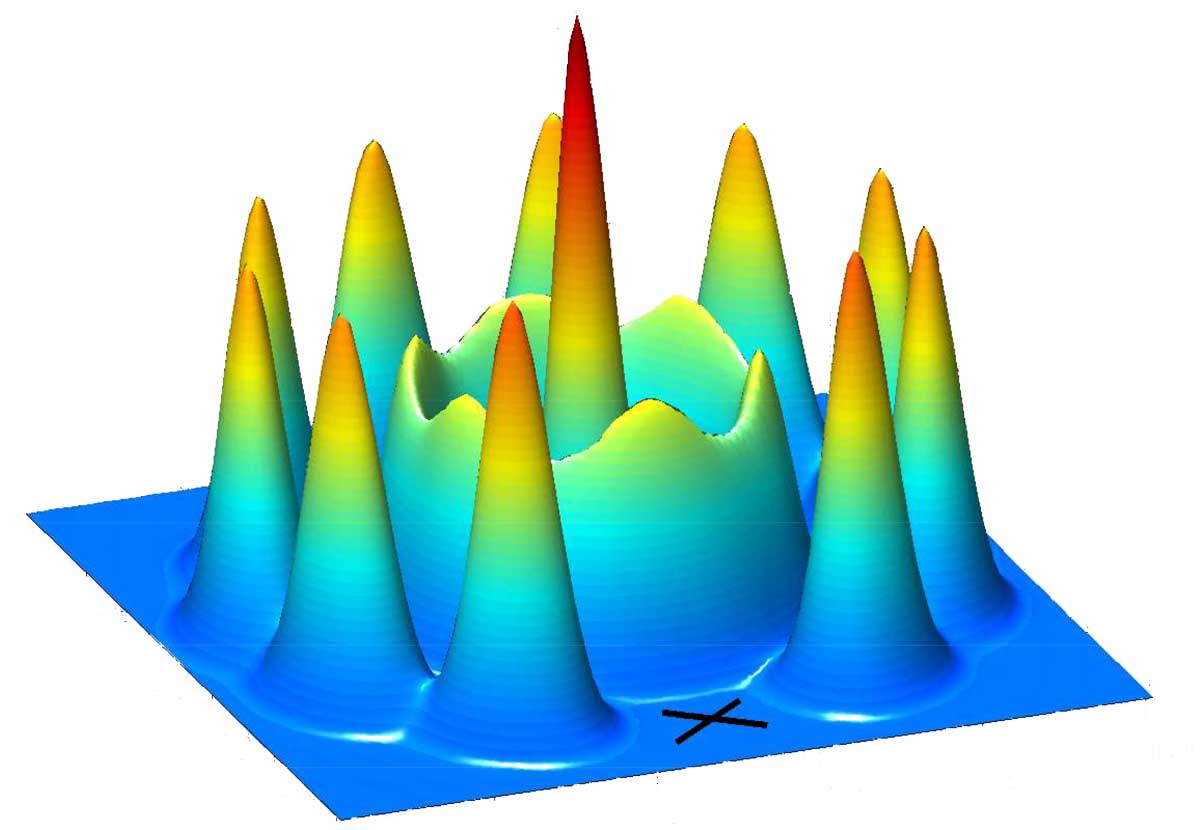
Pair density of 18-electron quantum dot
- novel forms of trial wave functions,
- optimization of linear and nonlinear wave function parameters in the presence of noise,
- more accurate imaginary time propagators,
- calculation forces on nuclei (a simple Hellman-Feynman approach does not work),
- evaluation of excited state energies,
- methods to ameliorate the Fermion sign problem,
- semistochastic projection, which combines the best features of exact diagonalization and quantum Monte Carlo methods.
There are three main classes of methods that are used for the study of electronic structure. The first class of methods are the quantum chemistry methods, the simplest of which, the Hartree-Fock method, is too crude an approximation for most problems of interest. The more sophisticated quantum chemistry methods, such as the configuration interaction method (expansion of the wave function as a linear combination of determinants) are prohibitively expensive for large systems. The second class of methods are the density functional methods. These contain an uncontrolled approximation for the "exchange-correlation" energy, so although they are adequate for many problems, there is no systematic way to improve them in those cases where greater accuracy is needed. We have concentrated on quantum Monte Carlo methods because they offer an excellent compromise between accuracy and computation time.
The methods we have developed are incorporated in a program called CHAMP (Cornell-Holland Abinitio Materials Package), that is being used by collaborators at other institutions.
Another area of interest for us in the past has been to employ quantum Monte Carlo calculations to compute nearly exact Kohn-Sham density functional quantities to study the deficiencies of the commonly used density functionals and to understand the relationship between Kohn-Sham eigenvalues and excitation energies for finite systems.
Current applications, that we are interested in, include the study of correlations of electrons in planar quantum dots subjected to magnetic fields, high-pressure phases and defects in semiconductors, spin states of transition metal atoms surrounded by ligands.
Some of our work is in collaboration with Garnet Chan in the Chemistry department at Princeton and with groups at the University of Paris, Duke, Rhode Island, Twente Universiteit, University of Basel, University of Erlangen and at SISSA, Trieste.